Category: Quantum

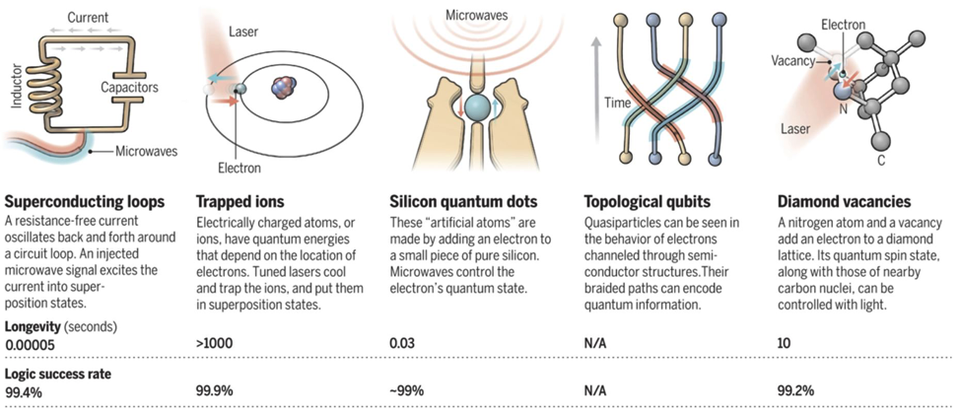
DIY: Physical Random Number Generators & Double Slit Experiment

paschmann

One of the benefits of Quantum Computing is their ability to generate truly random numbers.

Since classical computers are deterministic machines, governed by algorithms, they are inherently predictable. Therefor any number generated by a classical computer, even if it seems complex is actually based on a set of conditions or algorithm, which therefor makes it a “pseudo random number”, rather than truly random.

To generate truly random numbers you need to rely on a physical processor or phenomena that are unpredictable, examples of this include radioactive decay, electronic noise or even atmospheric noise.

Since QC is essentially based on a physical process and the probabilistic nature of quantum mechanics, its qubits can exist in a superposition state, this means they can represent a combination of 0 and 1 simultaneously, this state/property can be harnessed by QRNG (Quantum random number generators) to produce truly random numbers.

As a fun project, I decided to build a small physical QRNG using an Arduino, laser diode, beam splitter and two photo resistors. The basic premise is that you pulse the laser, it sends a wave/particle (both!) through the beam splitter, 50% of the time it should hit one of the two photo resistors, providing you with a random string of “1”s or “0”s.

While a very simple, basic and small example, it is a fun experiment. Check out OpenQbit.com if you would like to build your own. To make this a little easier, I laser cut a template/outline for the beam splitter for holding each of the components.

Enjoy Randomness? Check out these blog, sites, references: http://www.reallyreallyrandom.com

Non Quantum RNG generator using zener noise: http://www.reallyreallyrandom.com/zener/breadboard/

Nice video explaining the seed variables used and middle squares: https://www.khanacademy.org/computing/computer-science/cryptography/crypt/v/random-vs-pseudorandom-number-generators

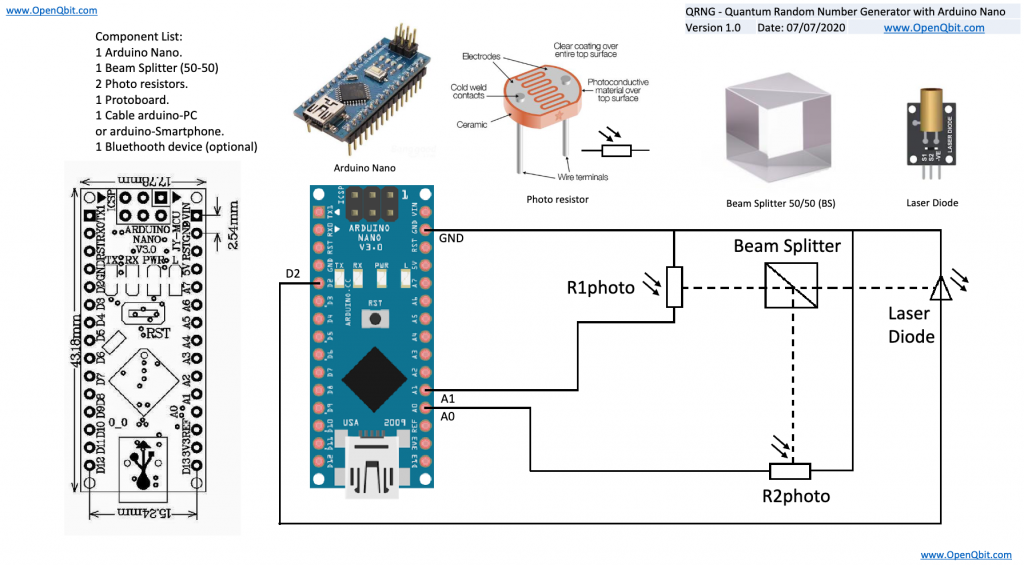
/* Annotated QRNGv1 Firmware V1.1 Author: Noah G. Wood Modified: Paul Aschmann Copyright (c) 2019 Spooky Manufacturing, LLC License: GPLv3.0 */ int triggerPin = 2; // This pin will pulse our quantum circuit int hPin = A0; // This pin measures the horizontal polarized photons int vPin = A1; // This pin measures the vertically polarized photons float H = 0; float V = 0; long previousMillis = 0; long interval = 1000; float maxH = 0; float maxV = 0; void setup() { // Just setting up triggerPin and serial connection //pinMode(13, OUTPUT); pinMode(triggerPin, OUTPUT); Serial.begin(9600); } int Random() { // Pulse the laser digitalWrite(triggerPin, HIGH); //delay(1); digitalWrite(triggerPin, LOW); } void loop() { // The main program // Run our program and print the random bit to serial //delay(1000); unsigned long currentMillis = millis(); if (currentMillis - previousMillis > interval) { previousMillis = currentMillis; Random(); } // Read the photoresistors H = analogRead(hPin); V = analogRead(vPin); // Determine random bit if (H > V) { // More photons in the H mode, return 0 Serial.println("-------------------- > H: "); Serial.println(H); Serial.println("V: "); Serial.println(V); if (H > maxH) { maxH = H; Serial.println("New max H"); } } else if (V > H) { // More photons in the V mode, return 1 Serial.println("-------------------- > V: "); Serial.println(V); Serial.println("H: "); Serial.println(H); if (V > maxV) { maxV = V; Serial.println("New max V"); } } else { Serial.println("Same values"); } delay(1000); } read more

Generating Random Numbers with QisKit & IBM Quantum Hardware

paschmann

Generating true random strings using classical computers is not as easy as you may think. Unlike deterministic processes that follow specific algorithms and patterns, achieving true randomness poses a challenge in the realm of classical computing. Classical computers operate based on predetermined instructions and logical operations, which inherently lack the inherent unpredictability required for true randomness.

In contrast, true randomness involves an element of unpredictability that goes beyond the deterministic nature of classical computing. Attempts to generate random strings on classical computers often involve algorithms that simulate randomness, but these are ultimately constrained by the deterministic nature of the underlying hardware and software. read more

Quantum Hardware – Notes

paschmann

Dilution Refrigerator, uses liquid helium
Absolute zero, optimal operating temp – 273 celcius

Top to bottom – different stages of cooling, filters, amplifiers

Sample holder holds quantum processor

CPU vs QPU

CPU – data/voltage/1’s 0’s flows through the gates (and, or, xor, etc.)
QPU – Data is on the chip, circuit is on the chip, pulses are sent to the chip 

chip created by lithography, metal deposition, all, oxide, etc.

Quantum Gates

Called block sphere
Pulses represent the gates.

Rotate qubit from ground state to 1
Example: Ex Pi rotation

Send another pulse, Pi/2

Quantum Entaglement

2 Qubits, and some interaction between them

When you entangle boxes, you can change probablities read more

DIY: Ion Trap Quantum Computer

paschmann
36C3: Build Your Own Quantum Computer At Home

An ion is a atom with one of the outer electrons removed (normally removed by pointing a laser beam at it) – forming positively charged ion.
Ion trapping is done in a vacuum chamber to isolate the ions from the external environment as much as possible. (And avoid other atoms in the air from bumping and

  • Atoms
    • Consist of 3 components, a proton and neutron (called the nucleus) in the center and electrons which orbit this nucleus
    • 117 different types
    • Are elements the same as atoms
    • Every element is unique and has an atomic number
      • That number tells you the number of protons in every atom of the element. The atomic number is also called the proton number.
        • read more

    • UC Berkley – Lecture Notes from Vazirani on Quantum Computing

    paschmann

    Notes: 

    Quantum Systems are exponentially powerful

    Based on particles: 2^500 – More particles in the universe

    Challenges:

    • Not all problems are well suited
    • Need to understand Q Mechanics

    Qubit – simplest quantum system

    Entanglement-

    • Bell Inequalities
    • Teleportation

    Lecture 1: Double Slit Experiment

    • Is light a particle or a wave?
    • If light was a particle, it would be like a bullet, and we would see the two beams overlap each other:
    • Strange that if both holes are open why we get this strange interference pattern.
    • Why did the count drop when both holes were open? From a decent amount, to nearly zero.
    • If we use bullets, we would see a whole number of bullets that get through
    • If we use water & waves, we get the same interference pattern.

    If we add a measuring device just after the slits to track which slit the electron goes through, it “disrupts” the measurement and we get the 2nd pattern. If we use a very slight/dim light enough light, we get the 3rd “expected” pattern, but we also miss a lot of the electrons and may not capture the pattern.

    = Hesienburgs uncertainty principle = Impossible to design apparatus which can detect which slit it went through without disturbing the interference pattern. read more

    Quantum Algorithms – Complexity Classes Notes

    paschmann

    Traveling sales person problem

    Solve problems which are NP hard – and they can’t be solved in polynomial time.

    P versus NP problem: full polynomial versus nondeterministic polynomial problem

    A P problem is one that can be solved in “polynomial time,” which means that an algorithm exists for its solution such that the number of steps in the algorithm is bounded by a polynomial function of n, where n corresponds to the length of the input for the problem. Thus, P problems are said to be easy, or tractable. A problem is called NP if its solution can be guessed and verified in polynomial time, and nondeterministic means that no particular rule is followed to make the guess. read more

    Bookmark: Quantum Links

    paschmann

    Good practical Python Quantum workbook

    https://livebook.manning.com/book/learn-quantum-computing-with-python-and-q-sharp/chapter-1/v-8/

    QCodes Github is what a lot of experimenters are using to control machines.

    https://github.com/QCoDeS/Qcodes

    Quantum Jobs

    https://medium.com/qiskit/the-hitchhiking-cats-guide-to-getting-a-job-in-quantum-computing-da7e3bb9ff64

    UC Berkley Course – Vazirani

    MIT Open Course on Quantum

    https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-845-quantum-complexity-theory-fall-2010/lecture-notes/

    Qiskit Hello

    https://mybinder.org/v2/gh/QISKit/qiskit-tutorial/master?filepath=community/games/Hello_Qiskit.ipynb read more