This was a fun 4 day program with the IBM Quantum Challenge. I probably spent +- 30 hours working through the 4 challenges, and during this time I recognized I really needed to learn more of the fundamental math aspects which Physics is built upon. In the end I completed all the work, the final challenge was a monster for someone with little theoretical knowledge in the field but after a few hints and tips from the team, I had a score which was acceptable.
This was the final requirements:
What circuit would make such a complicated unitary?
Is there some symmetry, or is it random? We just updated Qiskit with the introduction of a quantum circuit library (https://github.com/Qiskit/qiskit-terra/tree/master/qiskit/circuit/library). This library gives users access to a rich set of well-studied circuit families, instances of which can be used as benchmarks (quantum volume), as building blocks in building more complex circuits (adders), or as tools to explore quantum computational advantage over classical computation (instantaneous quantum polynomial complexity circuits).from qiskit import QuantumCircuit from may4_challenge.ex4 import check_circuit, submit_circuit
Using only single qubit rotations and CNOT gates, find a quantum circuit that approximates that unitary by a unitary up to an error , such that !
Note that the norm we are using here is the spectral norm, .
This can be seen as the largest scaling factor that the matrix has on any initial (normalized) state . One can show that this norm corresponds to the largest singular value of , i.e., the square root of the largest eigenvalue of the matrix , where denotes the conjugate transpose of .
When you submit a circuit, we remove the global phase of the corresponding unitary before comparing it with using the spectral norm. For example, if you submit a circuit that generates , we remove the global phase from before computing the norm, and you will have a successful submission. As a result, you do not have to worry about matching the desired unitary, , up to a global phase.
As the single-qubit gates have a much higher fidelity than the two-qubit gates, we will look at the number of CNOT-gates, , and the number of u3-gates, , to determine the cost of your decomposition as
Try to optimize the cost of your decomposition.
Note that you will need to ensure that your circuit is composed only of and gates. The exercise is considered correctly solved if your cost is smaller than 1600.
import qiskit.extensions.quantum_initializer.isometry as isometry
from qiskit.quantum_info.operators import Operator
import qiskit.compiler.transpile as transpile
from scipy.linalg import hadamard
from math import pi
qc = QuantumCircuit(4)
#apply hadamard using u3 gates
qc.u3(pi/2,0,pi,[0])
qc.u3(pi/2,0,pi,[1])
qc.u3(pi/2,0,pi,[2])
qc.u3(pi/2,0,pi,[3])
#k=HUH
Y=np.diag(k*np.exp(-2j*pi/3))
qc.diagonal(list(Y),[0,1,2,3])
qc.u3(pi/2,0,pi,[0])
qc.u3(pi/2,0,pi,[1])
qc.u3(pi/2,0,pi,[2])
qc.u3(pi/2,0,pi,[3])
qc3=transpile(qc, basis_gates=['u3', 'cx'],optimization_level=3)
check_circuit(qc3)
Circuit stats:
||U-V||_2 = 2.5785120546697708e-15
(U is the reference unitary, V is yours, and the global phase has been removed from both of them).
Cost is 51
Great! Your circuit meets all the constrains.
Your score is 51. The lower, the better!
Feel free to submit your answer and remember you can re-submit a new circuit at any time!
qc3.draw(output='mpl')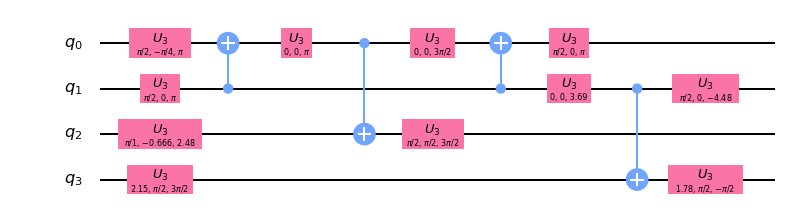
You must be logged in to post a comment.