LendingClub is a US peer-to-peer lending company headquartered in San Francisco, California, and has helped over 2.5 million customers simplify their finances in the last 10 years. LendingClub improves the loan process for borrows by offering a fast and easy online application. For investors, the company offers historical returns of 3 – 8% and anyone can invest with as little as $1000 [1].
Because LendingClub relies heavily on technology to evaluate their borrowers, getting an accurate risk analysis for each applicant requires systems which can quickly assess the applications, and upon approval, offer these loans to interested investors at a given interest rate. Of the $7.9 billion dollars loaned in 2018, $233 million was written off as defaulted loans. While this may seem insignificant at 2.9%, this does represent risks and losses which investors and the company would prefer to avoid. In order to mitigate risk, lending companies traditionally apply a fitting interest rate to each loan. For example, loans for a home or a car may have lower interest rates because the risk is reduced due to directly related collateral. In another example, someone with a poor credit history or having declared bankruptcy may have a higher interest rate due to the inherent risk of history repeating.
LendingClub provides an anonymized data set [2] of all their current and completed loans available for download on their website. Our goal was to use the data set to try and understand which data points may contribute to the interest rate designated to the loans. We reviewed the data set of 107,000+ observations (Appendix 1) and the accompanying data dictionary (Appendix 2) of the ~120 data categories included for each loan, and decided that we wanted to build a model which included 7 categories, resulting in 8 independent variables due to dummy variables, to try and predict if there is any relationship between these independent variables and the interest rate on the loan. This relationship could be described by the basic model Equation (1) below:
Int_rate = b0 – b1(loan_amount) + b2(funded_amount) – b3(annual_income) – b4(rent) – b5(last_payment_amount) + b6(debt_to_income_ratio) + b7(open_accounts) – b8(total_accounts) – b9(mortgage) (1)
Table 1: Independent variables include
| b1 | Loan Amount | The listed amount of the loan applied for by the borrower. If at some point in time, the credit department reduces the loan amount, then it will be reflected in this value. |
| b2 | Funded Amount | The total amount committed to that loan by investors. |
| b3 | Annual Income | The self-reported annual income provided by the borrower during registration. |
| b4 b9 | Home Ownership | Mortgage, Renter or Own |
| b5 | Last Payment Amount | The amount of the last payment made by the borrower |
| b6 | Debt to income ratio | A ratio calculated using the borrower’s total monthly debt payments on the total debt obligations, excluding mortgage and the requested LC loan, divided by the borrower’s self-reported monthly income. |
| b7 | Open accounts | The number of open credit lines in the borrower’s credit file. |
| b8 | Total Accounts | The total number of credit lines currently in the borrower’s credit file. |
Note: Home ownership was divided into to two dummy variables, mortgage and rent. Therefore, if both values are zero, the observation is for an individual who owns property outright.
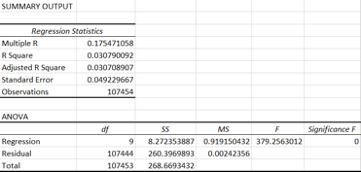
Table 2: Results Summary
Analysis of results
In initially looking at the overall results, we can take away a few points. After running our regression analysis on the data set, we found we had an R2 of 0.0308 using the stated independent variables. Traditionally, this is not a strong R2 value for cross sectional data. In general, the acceptable to excellent range for this type of data would be from 0.3 to 0.7. However, we can take a deeper look at the results to see if we can deduct any other information. Next, we can take a look at the F-test. The F-test tells us if the independent variables, as a group, explain a statistically significant share of variation in the dependent variable. Our results included an F (calculated value) and the test is shown below:
F-TEST:
Null hypothesis H0: R2 = 0
Alternative hypothesis HA: R2 > 0
The null can be stated alternatively as the model has explanatory power; the alternative is then that the model has no explanatory power.
If the value of F Calculated is greater than, or equal to the F Critical (From F Table) 1.88 (9 DoF x ∞ DoF) we can reject H0, if the value of F Calculated is less than F Critical we fail to reject H0.
In looking at the results, we find a calculated F value of 379 which is greater than the table value of 1.88. Therefore, we can reject H0. This implies that the model has explanatory power; however, we must look at several other factors before validating the model.
T-TEST:
Our next step is to look at each independent variable and its relationship to interest rate. This can be validated through a T-test, as shown below. These calculated t values shown in Table 3 are compared to the threshold value of 2.262.
Table 3: Estimate regression coefficients of interest rate relating to various variables
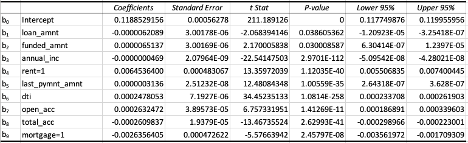
Null hypothesis H0: βi = 0
Alternative Hypothesis HA: βi ≠ 0
β = coefficient of variable being checked/Std Error of coefficient
If the absolute value of t Calculated is greater than or equal to t Critical (From the t Table) 2.262 (9 DoF x 0.05) we can reject H0, if the absolute value of t Calculated is less than the t Critical we fail to reject H0.
Comparing the t Critical value to each independent variable, we can see that we would reject H0 for annual income, home ownership status (rent/mortgage), last payment amount, debt to income ratio and both open and total accounts. On the other hand, we would fail to reject H0 for the variables loan amount and funded amount. These are calculated at the 95% confidence level.
P-TEST:
A third test that can be used to validate the model is the P test.
Null hypothesis H0: βi = 0
Alternative Hypothesis HA: βi ≠ 0
If the absolute value of the P value is less than or equal to 0.05, we can reject H0, if the P value is greater than 0.05, which is the P critical value, we fail to reject H0.
In reviewing the P values in Table 3, we can see that they all fall below the threshold of 0.05, or a confidence level equal to, or above 95%. This implies that all variables are relevant, contradicting some of our results from the T test shown above.
ELASTICITIES:
Elasticities were calculated in order to determine the magnitude of
effect of each independent variable on the dependent variable. Elasticity is
defined as the percent change in the dependent variable as a result of a
percent change in the independent variable.
The elasticities and formula are shown below in Table 4.
Table 4: Elasticities
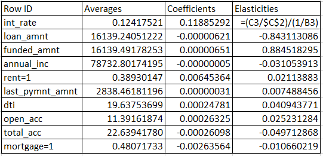
According to Table 4 above, the loan amount and funded amount have the greatest impact on the interest rate. The greatest impact is determined through the largest absolute value. The anomaly in this is that the loan amount variable has a negative elasticity and funded amount has a positive elasticity. This does not make sense given that most of the observations have the same value for these variables. It would make sense that the loan amount has a negative elasticity because a large loan amount generally lean towards something that contains equity, such as a car or house. These types of loans typically have lower interest rates and lower risk due to the availability of collateral. Alternatively, an account such as a credit card generally has a small balance and a high interest rate due to high risk and no collateral. Other interesting trends to note here would be the elasticities associated with open accounts and total accounts. A negative elasticity on open accounts is intuitive because if a person has many open accounts (large amounts of debt), risk is increased. Alternatively, a person with a large number of total accounts is assumed to have a lot of credit history and may be assumed to be less of a risk, therefore showing a negative elasticity.
Conclusion
In conclusion, the
model described above has some characteristics that are intuitive given the
input variables used; however the overall model is not great. The R2 value
is very low for cross-sectional data despite having passed the F-test. All of
the variables pass the P-test but a majority of them do not pass the T-test.
The model could be improved if other variables were available to test. Things
that might impact the interest rate could be credit score or the purpose of the
loan. We did have access to credit “grade” which we believe is related to
credit score, but these variables showed colinearity when included in the
model. Additionally, the data for “purpose of the loan” was available in the
data set, yet the inputs were not uniform. In order to include this in the
model, we would need to adjust the observation values for each of the 107,000
data points. Overall, we have a valid
model with plenty of room for improvement.
Appendix 1
Screenshot of example data set to be used.
Appendix 2
Included below is a sample of the data set, along with the metadata, explaining the fields, and the descriptions.
| Field | Description |
| acceptD | The date which the borrower accepted the offer |
| accNowDelinq | The number of accounts on which the borrower is now delinquent. |
| accOpenPast24Mths | Number of trades opened in past 24 months. |
| addrState | The state provided by the borrower in the loan application |
| all_util | Balance to credit limit on all trades |
| annual_inc_joint | The combined self-reported annual income provided by the co-borrowers during registration |
| annualInc | The self-reported annual income provided by the borrower during registration. |
| application_type | Indicates whether the loan is an individual application or a joint application with two co-borrowers |
| avg_cur_bal | Average current balance of all accounts |
| bcOpenToBuy | Total open to buy on revolving bankcards. |
| bcUtil | Ratio of total current balance to high credit/credit limit for all bankcard accounts. |
| chargeoff_within_12_mths | Number of charge-offs within 12 months |
| collections_12_mths_ex_med | Number of collections in 12 months excluding medical collections |
| creditPullD | The date LC pulled credit for this loan |
| delinq2Yrs | The number of 30+ days past-due incidences of delinquency in the borrower’s credit file for the past 2 years |
| delinqAmnt | The past-due amount owed for the accounts on which the borrower is now delinquent. |
| desc | Loan description provided by the borrower |
| dti | A ratio calculated using the borrower’s total monthly debt payments on the total debt obligations, excluding mortgage and the requested LC loan, divided by the borrower’s self-reported monthly income. |
| dti_joint | A ratio calculated using the co-borrowers’ total monthly payments on the total debt obligations, excluding mortgages and the requested LC loan, divided by the co-borrowers’ combined self-reported monthly income |
| earliestCrLine | The date the borrower’s earliest reported credit line was opened |
| effective_int_rate | The effective interest rate is equal to the interest rate on a Note reduced by Lending Club’s estimate of the impact of uncollected interest prior to charge off. |
| emp_title | The job title supplied by the Borrower when applying for the loan.* |
| empLength | Employment length in years. Possible values are between 0 and 10 where 0 means less than one year and 10 means ten or more years. |
| expD | The date the listing will expire |
| expDefaultRate | The expected default rate of the loan. |
| ficoRangeHigh | The upper boundary range the borrower’s FICO at loan origination belongs to. |
| ficoRangeLow | The lower boundary range the borrower’s FICO at loan origination belongs to. |
| fundedAmnt | The total amount committed to that loan at that point in time. |
| grade | LC assigned loan grade |
| homeOwnership | The home ownership status provided by the borrower during registration. Our values are: RENT, OWN, MORTGAGE, OTHER. |
| id | A unique LC assigned ID for the loan listing. |
| il_util | Ratio of total current balance to high credit/credit limit on all install acct |
| ils_exp_d | wholeloan platform expiration date |
| initialListStatus | The initial listing status of the loan. Possible values are – W, F |
| inq_fi | Number of personal finance inquiries |
| inq_last_12m | Number of credit inquiries in past 12 months |
| inqLast6Mths | The number of inquiries in past 6 months (excluding auto and mortgage inquiries) |
| installment | The monthly payment owed by the borrower if the loan originates. |
| intRate | Interest Rate on the loan |
| isIncV | Indicates if income was verified by LC, not verified, or if the income source was verified |
| listD | The date which the borrower’s application was listed on the platform. |
| loanAmnt | The listed amount of the loan applied for by the borrower. If at some point in time, the credit department reduces the loan amount, then it will be reflected in this value. |
| max_bal_bc | Maximum current balance owed on all revolving accounts |
| memberId | A unique LC assigned Id for the borrower member. |
| mo_sin_old_rev_tl_op | Months since oldest revolving account opened |
| mo_sin_rcnt_rev_tl_op | Months since most recent revolving account opened |
| mo_sin_rcnt_tl | Months since most recent account opened |
| mortAcc | Number of mortgage accounts. |
| msa | Metropolitan Statistical Area of the borrower. |
| mths_since_last_major_derog | Months since most recent 90-day or worse rating |
| mths_since_oldest_il_open | Months since oldest bank installment account opened |
| mths_since_rcnt_il | Months since most recent installment accounts opened |
| mthsSinceLastDelinq | The number of months since the borrower’s last delinquency. |
| mthsSinceLastRecord | The number of months since the last public record. |
| mthsSinceMostRecentInq | Months since most recent inquiry. |
| mthsSinceRecentBc | Months since most recent bankcard account opened. |
| mthsSinceRecentLoanDelinq | Months since most recent personal finance delinquency. |
| mthsSinceRecentRevolDelinq | Months since most recent revolving delinquency. |
| num_accts_ever_120_pd | Number of accounts ever 120 or more days past due |
| num_actv_bc_tl | Number of currently active bankcard accounts |
| num_actv_rev_tl | Number of currently active revolving trades |
| num_bc_sats | Number of satisfactory bankcard accounts |
| num_bc_tl | Number of bankcard accounts |
| num_il_tl | Number of installment accounts |
| num_op_rev_tl | Number of open revolving accounts |
| num_rev_accts | Number of revolving accounts |
| num_rev_tl_bal_gt_0 | Number of revolving trades with balance >0 |
| num_sats | Number of satisfactory accounts |
| num_tl_120dpd_2m | Number of accounts currently 120 days past due (updated in past 2 months) |
| num_tl_30dpd | Number of accounts currently 30 days past due (updated in past 2 months) |
| num_tl_90g_dpd_24m | Number of accounts 90 or more days past due in last 24 months |
| num_tl_op_past_12m | Number of accounts opened in past 12 months |
| open_acc_6m | Number of open trades in last 6 months |
| open_il_12m | Number of installment accounts opened in past 12 months |
| open_il_24m | Number of installment accounts opened in past 24 months |
| open_act_il | Number of currently active installment trades |
| open_rv_12m | Number of revolving trades opened in past 12 months |
| open_rv_24m | Number of revolving trades opened in past 24 months |
| openAcc | The number of open credit lines in the borrower’s credit file. |
| pct_tl_nvr_dlq | Percent of trades never delinquent |
| percentBcGt75 | Percentage of all bankcard accounts > 75% of limit. |
| pub_rec_bankruptcies | Number of public record bankruptcies |
| pubRec | Number of derogatory public records |
| purpose | A category provided by the borrower for the loan request. |
| reviewStatus | The status of the loan during the listing period. Values: APPROVED, NOT_APPROVED. |
| reviewStatusD | The date the loan application was reviewed by LC |
| revolBal | Total credit revolving balance |
| revolUtil | Revolving line utilization rate, or the amount of credit the borrower is using relative to all available revolving credit. |
| serviceFeeRate | Service fee rate paid by the investor for this loan. |
| subGrade | LC assigned loan subgrade |
| tax_liens | Number of tax liens |
| term | The number of payments on the loan. Values are in months and can be either 36 or 60. |
| title | The loan title provided by the borrower |
| tot_coll_amt | Total collection amounts ever owed |
| tot_cur_bal | Total current balance of all accounts |
| tot_hi_cred_lim | Total high credit/credit limit |
| total_bal_il | Total current balance of all installment accounts |
| total_cu_tl | Number of finance trades |
| total_il_high_credit_limit | Total installment high credit/credit limit |
| total_rev_hi_lim | Total revolving high credit/credit limit |
| totalAcc | The total number of credit lines currently in the borrower’s credit file |
| totalBalExMort | Total credit balance excluding mortgage |
| totalBcLimit | Total bankcard high credit/credit limit |
| url | URL for the LC page with listing data. |
| verified_status_joint | Indicates if the co-borrowers’ joint income was verified by LC, not verified, or if the income source was verified |
| zip_code | The first 3 numbers of the zip code provided by the borrower in the loan application. |
| revol_bal_joint | Sum of revolving credit balance of the co-borrowers, net of duplicate balances |
| sec_app_fico_range_low | FICO range (high) for the secondary applicant |
| sec_app_fico_range_high | FICO range (low) for the secondary applicant |
| sec_app_earliest_cr_line | Earliest credit line at time of application for the secondary applicant |
| sec_app_inq_last_6mths | Credit inquiries in the last 6 months at time of application for the secondary applicant |
| sec_app_mort_acc | Number of mortgage accounts at time of application for the secondary applicant |
| sec_app_open_acc | Number of open trades at time of application for the secondary applicant |
| sec_app_revol_util | Ratio of total current balance to high credit/credit limit for all revolving accounts |
| sec_app_open_act_il | Number of currently active installment trades at time of application for the secondary applicant |
| sec_app_num_rev_accts | Number of revolving accounts at time of application for the secondary applicant |
| sec_app_chargeoff_within_12_mths | Number of charge-offs within last 12 months at time of application for the secondary applicant |
| sec_app_collections_12_mths_ex_med | Number of collections within last 12 months excluding medical collections at time of application for the secondary applicant |
| sec_app_mths_since_last_major_derog | Months since most recent 90-day or worse rating at time of application for the secondary applicant |
| disbursement_method | The method by which the borrower receives their loan. Possible values are: CASH, DIRECT_PAY |
You must be logged in to post a comment.